class: middle, left, inverse, title-slide .title[ # Анализ мощности ] .subtitle[ ## Математические модели в зоологии ] .author[ ### Марина Варфоломеева ] .author[ ### Анастасия Лянгузова ] --- ## Экономим силы с помощью анализа мощности - Тестирование гипотез (двухвыборочный t-критерий) - Статистические ошибки при проверке гипотез - Мощность статистического теста - *A priori* анализ мощности, оценка величины эффекта - Как влиять на мощность тестов ### Вы сможете - сравнивать средние значения при помощи t-критерия, интерпретировать и описывать результаты - дать определение ошибок I и II рода, и графически изобразить их отношение к мощности теста - оценивать величину эффекта и необходимый объем выборки по данным пилотного исследования - загружать данные из .xlsx в R - строить графики средних значений со стандартными отклонениями с помощью `ggplot2` --- class: middle, center, inverse # Описательная статистика --- ## С какими данными мы работаем .pull-left[ .Large[Генеральная совокупность] ] .pull-right-33[ .Large[Выборка] ]  --- ## Как можно судить о свойствах генеральной совокупности по выборке? __Центральная предельная теорема__ (ЦПТ) говорит, что если мы возьмем достаточно большую выборку из генеральной совокупности, то среднее значение будет нормально распределено с параметрами `\(\mu_{\bar x}\)` и `\(\sigma _{\bar{x}}\)`: `$$\bar X \sim N (\mu_{\bar x}, \sigma_{\bar x})$$` При чем `\(\sigma_{\bar x} = \sigma/\sqrt{n}\)`. <br/> __Важно__: это так при больших объемах выборки ( `\(N > 30\)`, или даже `\(N > 100\)`), даже если `\(x\)` в генеральной совокупности не подчиняется нормальному распределению. Мы будем говорить о t-распределении, поскольку на самом деле ничего не знаем о `\(\sigma _{\bar{x}}\)` в генеральной совокупности. --- ## Характеризуем данные через связки описательных статистик .pull-left[ ### Центральные тенденции <br/>(Statistics of location) - Медиана (Median) - Среднее значение (Mean)] .pull-right[ ### Меры разброса <br/>(Statistics of dispersion) - Квантили (Quantiles) - Дисперсия (Variance), <br/>cтандартное отклонение (Standard Deviation)] --- ## Медиана и квантили в R Допустим, у нас есть некоторые измерения длины раковины раков-отшельников одного вида. Медиану можно увидеть зрительно, если отсортировать значения по возрастанию. ``` r shells <- c(10, 15, 14, 24, 27, 19, 31, 29, 26, 17) sort(shells) ``` ``` [1] 10 14 15 17 19 24 26 27 29 31 ``` Проверить, правильно ли мы нашли медиану, можно с помощью функции `median()`. ``` r median(shells) ``` ``` [1] 21.5 ``` --- ## Квантили Квантили бывают разные, в зависимости от того, на сколько частей они разделяют данные. - 2-квантиль --- медиана; - 4-квантиль --- квартили; - 100-квантиль --- перцентиль. --- ## Квантили в R Функция `quantile()` позволяет разделить наши данные на нужное число квантилей (задаются параметром `probs`). ``` r quantile(x = shells, probs = c(0.01, 0.25, 0.5, 0.75, 0.99)) ``` ``` 1% 25% 50% 75% 99% 10.36 15.50 21.50 26.75 30.82 ``` Можно использовать функцию и без указания значений `probs`, в таком случае функция посчитает *квартили*. ``` r quantile(shells) ``` ``` 0% 25% 50% 75% 100% 10.00 15.50 21.50 26.75 31.00 ``` --- ## Среднее и стандартное отклонение в R Среднее можно расчитать вручную. -- ``` r sum(shells) / length(shells) ``` ``` [1] 21.2 ``` -- Но есть и специальная функция в R, с помощью которой можно себя проверить. -- ``` r mean(shells) ``` ``` [1] 21.2 ``` --- ## Оценка разброса значений **Девиата** --- между значением вариаты (измерения) и средним: `$$x_i - \bar{x}$$` ``` r sh_deviates <- shells - mean(shells) sh_deviates ``` ``` [1] -11.2 -6.2 -7.2 2.8 5.8 -2.2 9.8 7.8 4.8 -4.2 ``` Не подходит для средней оценки разброса! --- ## Сумма квадратов и дисперсия Избавиться от знака девиаты можно, возведя значение в квадрат. Получим **сумму квадратов (Sum of Squares, SS)**. `$$SS = \sum{{(x_i - \bar{x})}^2} \ne 0$$` ``` r sum(sh_deviates^2) ``` Чтобы получить **дисперсию**, делим `SS` на **число степеней свободы (degrees of freedom)** (n - 1). ``` r sum(sh_deviates^2) / (length(shells) - 1) var(shells) ``` --- ## Стандартное/среднеквадратичное отклонение **Стандартное отклонение** --- корень из дисперсии. Позволит вернуться к исходным единицам измеренния, а также может быть изображено на графике. `$$s = \sqrt{s^2} = \sqrt{\frac{\sum{(x_i - \bar{x})^2}}{n - 1}} = SD$$` Стандартное отклонение --- это средняя величина отклонения, и ее уже можно изобразить на графике. ``` r sqrt(sum(sh_deviates^2) / (length(shells) - 1)) ``` ``` [1] 7.146 ``` ``` r sd(shells) ``` ``` [1] 7.146 ``` --- ## Визуализация описательных статистик Превращаем рачков-дурачков в датафрейм для визуализации. ``` r shells_data <- data.frame(length = shells) ``` .pull-left[ ### Медиана и квартили ``` r ggplot(data = shells_data) + geom_boxplot(aes(x = 'Медиана \nи квантили', y = length)) ``` 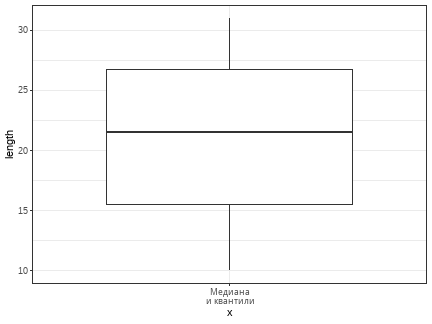<!-- --> ] .pull-right[ ### Среднее и ст. отклонение ``` r ggplot(data = shells_data) + stat_summary(geom = 'pointrange', fun.data = mean_sdl, fun.args = list(mult = 1), aes(x = 'Среднее \nи стандартное отклонение', y = length)) ``` 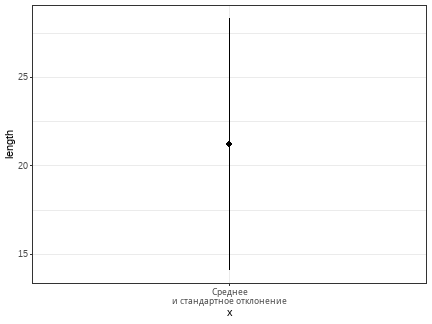<!-- --> ] --- ## Особенности применения связок центральные тенденции --- меры разброса - работают только в связке (медиана --- квантили; среднее --- стандартное отклонение); - медиана устойчива к выбросам, в отличие от среднего; - связка "медиана --- квантили" может быть применена к данным с любой формой распределения в отличие от "среднее --- стандартное отклонение". --- class: middle, center, inverse # Нормальное распределение --- ## Нормальное распределение .pull-left-66[ 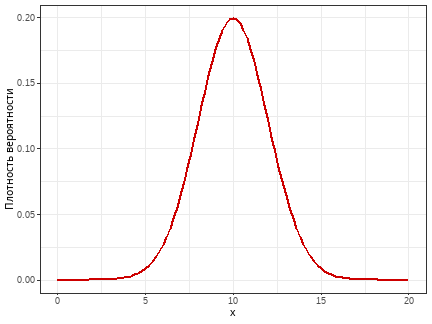<!-- --> ] .pull-right-33[ - симметричное - унимодальное - непрерывное ] .pull-left-66[ `$$f(x) = \cfrac {1}{\sigma \sqrt{2 \pi}} \; e^{- \: \cfrac{(x-\mu)^2}{2\sigma^2}}$$` - `\(\mu\)` --- среднее значение; - `\(\sigma\)` --- стандартное отклонение. Это кратко записывается как `\(x \sim N(\mu, \sigma)\)`. ] --- ## Вероятности --- это площади под кривой распределения <!-- --> `\(-\infty < x < +\infty\)`. Площадь под всей кривой `\(= 1\)`. Вероятность встречи значений из определенного промежутка можно узнать, проинтегрировав функцию распределения. --- ## Эмпирическое правило нормального распределения .center[  ] - 68% значений находятся в пределах 1 стандартного отклонения `\(\sigma\)` - 95% значений --- в пределах 2 `\(\sigma\)` - 99.7% значений --- в пределах 3 `\(\sigma\)` --- class: middle, center, inverse # Тестирование гипотез --- ## Тестирование гипотез: основные принципы 1. Формулировка **нулевой гипотезы** (`\(H_0\)`). Обычно это гипотеза об отсутствии разницы или связи между параметрами в генеральной совокупности (например, об отсутствии разницы между средними). 2. Формулировка **альтернативной гипотезы** (`\(H_A\)`) --- гипотезы, являющейся правдивой в случае отвержения `\(H_0\)`. 3. Выбор статистического теста для проверки нулевой гипотезы. Одна из популярнейших статистик для проверки гипотезы о разницы в средних --- **t-статистика**. 4. Определение уровня значимости &\alpha& (p-value) для нашей гипотезы. --- ## t-распределение --- распределение разницы средних для выборок из одной совокупности t-статистика подчиняется t-распределению. Иными словами, если много раз взять выборки __из одной__ совокупности (т.е. __при условии, что `\(H_0\)` верна__) и посчитать между ними разницу, то она будет подчиняться t-распределению. Форма t-распределения зависит только от одного параметра --- числа степеней свободы `\(df\)`. <!-- --> --- ## В хвостах этого распределения находятся редкие значения (__для случая, когда `\(H_0\)` верна__) <!-- --> Обычно используется уровень значимости `\(\alpha\)` 0.05 или 0.01. __Уровень значимости `\(\alpha\)` --- это вероятность ошибочно отвергнуть справедливую нулевую гипотезу__. Т.е. это вероятность найти различия там, где их нет (__вероятность ошибки I рода__). Для t-теста `\(\alpha\)` --- это вероятность ошибочно сделать вывод о том, что средние выборок различаются __при условии, что эти выборки получены из одной генеральной совокупности__. --- ## Тест Стьюдента (t-критерий) Гипотезы: `\(H_0: \mu_1 - \mu_2 = 0\)`, `\(H_A: \mu_1 - \mu_2 \ne 0\)` .pull-left-66[ Двухвыборочный тест Стьюдента (Student, 1908) используется для проверки значимости различий между средними значениями двух величин. `$$t= \frac{\bar{x}_1 - \bar{x}_2}{SE_{\bar{x}_1 - \bar{x}_2}}$$`] .pull-right-33[  .tiny[William Sealy Gosset. Photo: Wikipedia] ] Условия применимости: - Наблюдения случайны и независимы друг от друга - Выборки случайны и независимы друг от друга - Величины нормально распределены или большая выборка (> 30 наблюдений в группе) - __Дисперсии в группах одинаковы__ `\(SE = \sqrt{\frac{s_1^2(n_1-1) +s_2^2(n_2-1)}{n_1+n_2-2}\Big(\frac{1}{n_1} + \frac{1}{n_2}\Big)}\)` `\(df = (n_1 - 1) + (n_2 - 1) = n_1 + n_2 - 2\)` --- ## t-тест Уэлча (Welch, 1938, 1947) --- это модификация теста Стьюдента __для случая разных дисперсий__ .pull-left-66[ `$$t= \frac{\bar{x}_1 - \bar{x}_2}{SE_{\bar{x}_1 - \bar{x}_2}}$$` Условия применимости: - Наблюдения случайны и независимы друг от друга - Выборки случайны и независимы друг от друга - Величины нормально распределены или большая выборка (> 30 наблюдений в группе) ] .pull-right-33[  .tiny[Bernard Lewis Welch. Photo scanned by GeneralBurgoyne on Reddit] ] `\(SE = \sqrt{{s_1^2}/ {n_1} + {s_2^2}/{n_2}}\)` Приблизительное число степеней свободы рассчитывается по уравнению Уэлча-Саттеруэйта `$$df \approx \cfrac {({s^2_{1}}/{n_{1}} + {s^2_{x_2}}/{n_{2}})^2} {\frac{1}{n_{1} - 1}\bigg(\frac {s_{1}^2} {n_{1}}\bigg)^2 + \frac{1}{n_{2} - 1}\bigg(\frac {s_{2}^2} {n_{2}}\bigg)^2}$$` --- ## Тестирование гипотезы о равенстве двух средних при помощи t-теста <!-- --> 1. Для конкретных данных считаем значение t-критерия. 2. Сравниваем его с теоретическим распределением t (распределением при условии, что `\(H_0\)` верна). 3. Принимаем решение, отвергнуть ли `\(H_0\)`. --- ## Одновыборочный и двухвыборочный t-test Альтернативная гипотеза может быть сформулирована по-разному. В зависимости от её формулировки приходим к разным вариантам t-теста. .pull-left[ ### Односторонний тест Формулировка `\(H_A\)` имеет некую направленность (например, что средние в одной из групп больше, чем в другой). <!-- --> ] .pull-right[ ### Двухсторонний тест Формулировка `\(H_A\)` не направлена и говорит о наличии различий/взаимосвязи (например, средние в группах сравнения отличны). <!-- --> ] --- ## Пример: Гормоны и артериальная гипертензия Синдром Кушинга --- это нарушения уровня артериального давления и целый комплекс других симптомов, вызванных гиперсекрецией кортизола надпочечниками. .center[  .tiny[Cushing’s syndrome. Photo: Wikipedia] ] --- ## Пример: Гормоны и артериальная гипертензия В датасете `Cushings` (пакет `MASS`) записаны данные о секреции двух метаболитов при разных типах синдрома (данные из кн. Aitchison, Dunsmore, 1975). - `Tetrahydrocortisone` --- секреция тетрагидрокортизона с мочой (мг/сут.) - `Pregnanetriol` --- секреция прегнантриола с мочой (мг/сут.) - `Type` --- тип синдрома: - `a` --- аденома - `b` --- двусторонняя гиперплазия - `c` --- карцинома - `u` --- не известно Различается ли секреция тетрагидрокортизона при аденома и двусторонней гиперплазии надпочечников? ``` r library(MASS) data("Cushings") ``` --- ## Двухвыборочный t-критерий в R рассчитывает функция `t.test()` О параметрах функции t.test() можно прочесть в справке `?t.test`. -- Если в данных __ровно две группы__ используется т.н. "формула". ``` t.test(formula = зависимая_переменная ~ группирующая_переменная, data = датафрейм_с_данными, ...) ``` -- Если __больше двух групп__ - можно непосредственно передать их данные в виде векторов, ``` t.test(x = вектор_1_группа, y = вектор_2_группа, ...) ``` -- - либо можно отобрать ровно две группы при помощи аргумента `subset`. ``` t.test(formula = зависимая_переменная ~ группирующая_переменная, data = датафрейм_с_данными, subset = логический_вектор_отбирающий_2_группы, ...) ``` --- ## Различается ли секреция тетрагидрокортизона при аденома и двусторонней гиперплазии надпочечников? ``` r tt <- t.test(formula = Tetrahydrocortisone ~ Type, data = Cushings, subset = Cushings$Type %in% c('a', 'b')) tt ``` ``` Welch Two Sample t-test data: Tetrahydrocortisone by Type t = -4.1, df = 11, p-value = 0.002 alternative hypothesis: true difference in means between group a and group b is not equal to 0 95 percent confidence interval: -7.988 -2.438 sample estimates: mean in group a mean in group b 2.967 8.180 ``` -- Результаты можно описать, например, так: - Секреция тетрагидрокортизона значимо различается у пациентов с аденомой и двусторонней гиперплазией надпочечников (`\(t_{10.69} = -4.15\)`, `\(p = <0.05\)`) --- ## Задания 1-3 __Задание 1__ Перепишите вызов функции `t.test()` с использованием другого шаблона вызова (с параметрами `x` и `y`). __Задание 2__ Как называются отдельные элементы результатов можно узнать посмотрев их структуру при помощи функции `str()`. __Задание 3__ Получите отдельные элементы результатов из объекта `tt` при помощи оператора `$`: - значение t-критерия; - число степеней свободы; - уровень значимости. --- ## Другой шаблон вызова функции `t.test()` ``` r tt <- t.test(x = Cushings$Tetrahydrocortisone[Cushings$Type == 'a'], y = Cushings$Tetrahydrocortisone[Cushings$Type == 'b']) tt ``` ``` Welch Two Sample t-test data: Cushings$Tetrahydrocortisone[Cushings$Type == "a"] and Cushings$Tetrahydrocortisone[Cushings$Type == "b"] t = -4.1, df = 11, p-value = 0.002 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -7.988 -2.438 sample estimates: mean of x mean of y 2.967 8.180 ``` --- ## Что спрятано в результатах? Как называются отдельные элементы результатов можно узнать посмотрев их структуру при помощи функции `str()`. ``` r str(tt) ``` ``` List of 10 $ statistic : Named num -4.15 ..- attr(*, "names")= chr "t" $ parameter : Named num 10.7 ..- attr(*, "names")= chr "df" $ p.value : num 0.00172 $ conf.int : num [1:2] -7.99 -2.44 ..- attr(*, "conf.level")= num 0.95 $ estimate : Named num [1:2] 2.97 8.18 ..- attr(*, "names")= chr [1:2] "mean of x" "mean of y" $ null.value : Named num 0 ..- attr(*, "names")= chr "difference in means" $ stderr : num 1.26 $ alternative: chr "two.sided" $ method : chr "Welch Two Sample t-test" $ data.name : chr "Cushings$Tetrahydrocortisone[Cushings$Type == \"a\"] and Cushings$Tetrahydrocortisone[Cushings$Type == \"b\"]" - attr(*, "class")= chr "htest" ``` --- ## Можно получить элементы результатов в виде отдельных цифр ``` r tt$parameter # степени свободы ``` ``` df 10.69 ``` ``` r tt$p.value # уровень значимости ``` ``` [1] 0.001719 ``` ``` r tt$statistic # значение t-критерия ``` ``` t -4.15 ``` --- class: middle, center, inverse # Статистические ошибки при проверке гипотез --- ## Типы ошибок при проверке гипотез | |$$H0 == TRUE$$ | `$$H0 == FALSE$$` | |-----|-----|-----| | Отклонить `\(H_0\)` | Ошибка I рода | Верно | | Сохранить `\(H_0\)` | Верно | Ошибка II рода | --- ## Ошибка I рода | |$$H0 == TRUE$$ | `$$H0 == FALSE$$` | |-----|-----|-----| | Отклонить `\(H_0\)` | Ошибка I рода | Верно | | Сохранить `\(H_0\)` | Верно | Ошибка II рода | <!-- --> __Ошибка I рода --- вероятность отвергнуть `\(H_0\)`, когда верна `\(H_0\)`.__ --- ## Мы этого не знаем, но может быть верна `\(H_A\)`... | |$$H0 == TRUE$$ | `$$H0 == FALSE$$` | |-----|-----|-----| | Отклонить `\(H_0\)` | Ошибка I рода | Верно | | Сохранить `\(H_0\)` | Верно | Ошибка II рода | <!-- --> Можно построить еще одно распределение статистики --- распределение, при условии того, что верна `\(H_A\)`. --- ## Ошибка II рода | |$$H0 == TRUE$$ | `$$H0 == FALSE$$` | |-----|-----|-----| | Отклонить `\(H_0\)` | Ошибка I рода | Верно | | Сохранить `\(H_0\)` | Верно | Ошибка II рода | <!-- --> __Ошибка II рода --- вероятность принять `\(H_0\)`, когда верна__ `\(H_A\)`. --- ## Верные и неверные решения .pull-left[ **Ошибка I рода: нашли то, чего нет** ] .pull-right[ **Ошибка II рода: не нашли то, что было** ] | | `\(H_0\)` верна | `\(H_0\)` неверна | |:-----:|:-----:|:-----:| | Отклонить H0 | Ошибка I рода с вероятностью <span class="orange">&alpha;</span></br>Ложно-положительный результат | Верно | | Сохранить H0 | Верно | Ошибка II рода с вероятностью <span class= "blue">&beta;</span> </br> Ложно-отрицательный результат | --- ## Мощность теста --- способность выявлять различия | |$$H0 == TRUE$$ | `$$H0 == FALSE$$` | |-----|-----|-----| | Отклонить `\(H_0\)` | Ошибка I рода | Верно | | Сохранить `\(H_0\)` | Верно | Ошибка II рода | <!-- --> __Мощность теста - вероятность отвергнуть `\(H_0\)`, когда верна__ `\(H_A\)`: `\(Power = 1 - \beta\)`, где `\(\beta\)` --- вероятность ошибки II рода (не найти различия там, где они есть). --- ## Мощность теста `$$Power = 1 - \beta$$` Обычно считается, что хорошо, когда мощность не меньше 0.8. Т.е. что в 80% случаев мы можем найти различия заданной величины, если они есть. <!-- --> --- ## Анализ мощности .pull-left[ *A priori* - какой нужен объем выборки, чтобы найти различия с разумной долей уверенности? - различия какой величины мы можем найти, если известен объем выборки? ] .pull-right[ *Post hoc* - смогли бы мы найти различия при помощи нашего эксперимента `\((\alpha\)`, `\(n\)`), если бы величина эффекта была `\(X\)`? ] --- class: middle, center, inverse # A priory анализ мощности --- ## A priori анализ мощности .pull-left[ Что нужно - тест - уровень значимости - желаемая мощность теста - ожидаемая величина эффекта ] -- .pull-right[ Что есть - `\(t\)`-критерий - `\(\alpha = 0.05\)` - `\(Power = 0.8\)` - ? ] --- ## Величина эффекта .pull-left-66[ `\(d\)` Коэна (Cohen's d) `$$d = \frac{\bar x_1 - \bar x_2}{SD_{pooled}}$$` где `\(SD_{pooled}\)` --- обобщенное стандартное отклонение (расчитывается для каждой из групп сравнения). `$$SD_{pooled} = {\sqrt{\frac {(n _1 - 1)s_1^2 + (n _2 - 1)s_2^2 } {n _1 + n _2 - 2} } }$$` ] .pull-right-33[  .tiny[ Jacob Cohen] ] --- ## Величина эффекта Яков Коэн предложил делить эффекты на сильные, умеренные и слабые (Cohen, 1982) ``` r library(pwr) cohen.ES(test = 't', size = 'large') ``` ``` Conventional effect size from Cohen (1982) test = t size = large effect.size = 0.8 ``` --- ## Расчет объема выборки для обнаружения эффекта известной величины Функции для анализа мощности t-критерия: - при одинаковых объемах групп `pwr.t.test()` - при разных объемах групп `pwr.t2n.test()` Какая нужна выборка, чтобы обнаружить _сильный эффект_ с вероятностью 0.8 при уровне значимости 0.05? ``` r pwr.t.test(n = NULL, d = 0.8, power = 0.8, sig.level = 0.01, type = 'two.sample', alternative = 'two.sided') ``` ``` Two-sample t test power calculation n = 38.19 d = 0.8 sig.level = 0.01 power = 0.8 alternative = two.sided NOTE: n is number in *each* group ``` --- ## Задание 4 Какая нужна выборка, чтобы обнаружить _слабый эффект_ с вероятностью 0.8 при уровне значимости 0.05? Вам понадобятся функции `cohen.ES()` и `pwr.t.test()` --- ## Решение ``` r cohen.ES(test = 't', size = 'small') # величина слабого эффекта по Коэну ``` ``` Conventional effect size from Cohen (1982) test = t size = small effect.size = 0.2 ``` ``` r # Какой нужен объем выборки? pwr.t.test(n = NULL, d = 0.2, power = 0.8, sig.level = 0.05, type = 'two.sample', alternative = 'two.sided') ``` ``` Two-sample t test power calculation n = 393.4 d = 0.2 sig.level = 0.05 power = 0.8 alternative = two.sided NOTE: n is number in *each* group ``` Для того, чтобы при помощи t-теста обнаружить слабый эффект (d = 0.2) с вероятностью 0.8 и при уровне значимости 0.05, нужно собрать выборку не меньше 394 наблюдений __в каждой__ группе. --- class: middle, center, inverse # A priory анализ мощности по данным пилотного исследования --- ## Пример: Морфометрия жуков-листоедов Измерения 43 самцов жуков-листоедов двух видов жуков из подсемейства козявок (Galerucinae) в семействе листоедов (Chrysomelidae): _Chaetocnema concinna_ (на фото), _Ch. heptapotamica_. .pull-left-33[  .tiny[_Chaetocnema concinna_. Photo: Udo Shmidt on Flickr] ] .pull-right-66[ Переменные - fjft --- ширина первого членика первой лапки в микронах (сумма измерений для обеих лапок) - species --- вид жуков (1 --- *Ch. concinna*, 2 --- *Ch. heptapotamica*) ] Есть ли морфологические различия между видами? ``` r library(readxl) flea <- read_excel(path = 'data/fleabeetles-subset.xlsx', sheet = 'dat') ``` .tiny[Фрагмент данных из работы Lubischew, A.A., 1962. On the use of discriminant functions in taxonomy. Biometrics, pp.455-477.] --- ## Все ли правильно открылось? ``` r str(flea) # Структура данных ``` ``` tibble [43 × 2] (S3: tbl_df/tbl/data.frame) $ fjft : num [1:43] 191 185 200 173 171 160 188 186 174 163 ... $ species: num [1:43] 1 1 1 1 1 1 1 1 1 1 ... ``` ``` r head(flea) # Первые несколько строк файла ``` ``` # A tibble: 6 × 2 fjft species <dbl> <dbl> 1 191 1 2 185 1 3 200 1 4 173 1 5 171 1 6 160 1 ``` --- ## Делаем фактором переменную, где записан вид ``` r flea$species <- factor(flea$species, levels = c(1, 2), labels = c('cocin', 'hept')) ``` --- ## Знакомимся с данными Есть ли пропущенные значения? ``` r colSums(is.na(flea)) ``` ``` fjft species 0 0 ``` Каковы объемы выборок? Поскольку нет пропущенных значений, можно посчитать так: ``` r table(flea$species) ``` ``` cocin hept 21 22 ``` --- ## Представим, что это данные пилотного исследования Мы хотим выяснить, сколько нужно жуков, чтобы показать, что ширина первого членика первой лапки различается у этих двух видов. График средних и стандартных отклонений. ``` r library(ggplot2) theme_set(theme_bw()) ggplot(data = flea, aes(x = species, y = fjft)) + stat_summary(geom = 'pointrange', fun.data = mean_sdl) + labs(y = 'Ширина первого членика \nпервой лапки (мкм)', x = 'Вид') ``` <!-- --> --- ## Величина эффекта по исходным данным ``` r library(effsize) eff_flea <- cohen.d(d = flea$fjft, f = flea$species) eff_flea ``` ``` Cohen's d d estimate: 4.154 (large) 95 percent confidence interval: lower upper 3.059 5.248 ``` Вычислим модуль, поскольку для `pwr.t.test()` эффект должен быть положительным. ``` r effect_size_flea <- abs(eff_flea$estimate) ``` --- ## Задание 5 Рассчитайте объем выборки, чтобы показать различия размеров с вероятностью 0.8 на уровне значимости 0.05 Используйте функцию `pwr.t.test()` --- ## Решение ``` r pwr_flea <- pwr.t.test(n = NULL, d = effect_size_flea, power = 0.8, sig.level = 0.05, type = 'two.sample', alternative = 'two.sided') pwr_flea ``` ``` Two-sample t test power calculation n = 2.354 d = 4.154 sig.level = 0.05 power = 0.8 alternative = two.sided NOTE: n is number in *each* group ``` -- - Нужна выборка из __3 жуков каждого вида__, чтобы с вероятностью 0.8 обнаружить различия размеров между видами. --- class: middle, center, inverse # Как влиять на мощность теста? --- ## Чем больше объем выборки --- тем больше мощность <!-- --> --- ## Чем больше уровень значимости --- тем больше мощность <!-- --> --- ## Чем больше величина различий --- тем больше мощность <!-- --> --- ## Каким образом можно повлиять на мощность теста? - Мощность теста можно регулировать, если - изменить число повторностей - выбрать другой уровень значимости `\(\alpha\)` - определиться, какие эффекты действительно важны `\(ES\)` --- ## Take-home messages - Чтобы не находить несуществующих эффектов, фиксируем уровень значимости. - Чтобы не пропустить значимое, рассчитываем величину эффекта, объем выборки и мощность теста. - Способность выявлять различия зависит: - от объема выборки, - от уровня значимости - от величины эффекта. --- ## Дополнительные ресурсы - Quinn, Keough, 2002, pp. 164-170 - OpenIntro: Statistics - Sokal, Rohlf, 1995, pp. 167-169. - Zar, 1999, p. 83. - [R Data Analysis Examples - Power Analysis for Two-group Independent sample t-test. UCLA: Statistical Consulting Group.](http://www.ats.ucla.edu/stat/r/dae/t_test_power2.htm) - [R Data Analysis Examples - Power Analysis for One-sample t-test. UCLA: Statistical Consulting Group.](http://www.ats.ucla.edu/stat/r/dae/t_test_power.htm) - [FAQ - How is effect size used in power analysis? UCLA: Statistical Consulting Group.](http://www.ats.ucla.edu/stat/mult_pkg/faq/general/effect_size_power/effect_size_power.htm)